Математика и информатика
Лекция 4
Основы теории вероятностей и математической статистики
План
1. Основы теории вероятностей 1.1. Случайный эксперимент, элементарные исходы, события 1.2. Классическое определение вероятности1.1. Случайный эксперимент, элементарные исходы, события
Случайным (стохастическим) экспериментом или испытанием называется осуществление какого-либо комплекса условий, который можно практически или мысленно воспроизвести сколь угодно большое число раз.
Примеры случайного эксперимента: подбрасывание монеты или игральной кости (кубика), извлечение одной карты из перетасованной колоды.
Явления, происходящие при реализации этого комплекса условий, то есть в результате случайного эксперимента, называются элементарными исходами. Считается, что при проведении случайного эксперимента реализуется только один из возможных элементарных исходов.
Если монету подбросить один раз, то элементарными исходами можно считать выпадение герба (Г) или цифры (Ц).
Если случайным экспериментом считать троекратное подбрасывание монеты, то элементарными исходами можно считать следующие:
ГГГ, ГГЦ, ГЦГ, ЦГГ, ГЦЦ, ЦГЦ, ЦЦГ, ЦЦЦ.
Множество всех элементарных исходов случайного эксперимента называется пространством элементарных исходов. Будем обозначать пространство элементарных исходов буквой W (омега большая)
i-й элементарный исход будем обозначать w i (w – омега малая).Если пространство элементарных исходов содержит
n элементарных исходов, тоW =(w 1, w 2 ,..., w n).
Для троекратного подбрасывания монеты,
W
=(ГГГ, ГГЦ, ...ЦЦЦ).Если случайный эксперимент – подбрасывание игральной кости, то W
=(1,2,3,4,5,6).Если
W конечно или счетно, то случайным событием или просто событием называется любое подмножество W .Множество называется счетным, если между ним и множеством
N натуральных чисел можно установить взаимно-однозначное соответствие.Пример счетного множества: множество возможных значений времени прилета инопланетян на Землю, если время отсчитывать с настоящего момента и исчислять с точностью до секунды.
Примеры несчетных множеств: множество точек на заданном отрезке, множество чисел
x, удовлетворяющих неравенству 1< x £ 2.В случае несчетного множества W будем называть событиями только подмножества, удовлетворяющие некоторому.
Приведем примеры событий. Пусть бросается игральная кость, и элементарным исходом считается выпавшее число очков: W
=(1,2,3,4,5,6). A – событие, заключающееся в том, что выпало четное число очков: А=(2,4,6); B – событие, заключающееся в том, что выпало число очков, не меньшее 3-х: B=(3,4,5,6).Говорят, что те исходы, из которых состоит событие А
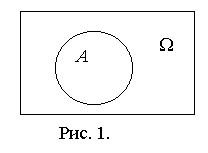
, благоприятствуют событию А.События удобно изображать в виде рисунка, который называется диаграммой Венна. На рисунке 1 пространство элементарных исходов W изображено в виде прямоугольника, а множество элементарных исходов, благоприятствующих событию
A, заключено в эллипс. Сами исходы на диаграмме Венна не изображаются, а информация о соотношении между их множествами содержится в расположении границ соответствующих областей.
Сумма, произведение, разность событий.
Подробнее>>1.2. Классическое определение вероятности
Возможна ситуация, когда пространство элементарных исходов состоит из конечного числа
N элементарных исходов, причем случайный эксперимент таков, что вероятности осуществления каждого из этих N элементарных исходов представляются равными. Примеры таких случайных экспериментов: подбрасывание симметричной монеты, бросание правильной игральной кости, случайное извлечение игральной карты из перетасованной колоды. В силу введенной аксиомы вероятность каждого элементарного исхода в этом случае равна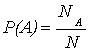
. Из этого следует, что если событие А содержит NA элементарных исходов, вероятность события определяется как отношение числа благоприятных исходов к общему числу всех возможных исходов:
Т.к. число благоприятных исходов не может быть больше числа всех исходов, то численное значение вероятности лежит в пределах
.
Пример 1.
Какова вероятность выпадения подряд двух раз герба при троекратном подбрасывании монеты?Как было сказано выше, всего элементарных исходов 8:
ГГГ, ГГЦ, ГЦГ, ЦГГ, ГЦЦ, ЦГЦ, ЦЦГ, ЦЦЦ.
Из них удовлетворяющих нас исходов будет 3 Следовательно вероятность того что при троекратном бросании монеты два раза подряд выпадет герб равна 3
/8.Пример 2
. Из набора, содержащего 10 одинаковых на вид электроламп, среди которых 4 бракованных, случайным образом выбирается 5 ламп. Какова вероятность, что среди выбранных ламп будут 2 бракованные?Прежде всего, отметим, что выбор любой пятерки ламп имеет одну и ту же вероятность. Всего существует 
(см. лек. 3 о числе сочетаний) способов составить такую пятерку, то есть случайный эксперимент в данном случае имеет равновероятных исходов.
Сколько из этих исходов удовлетворяют условию “в пятерке две бракованные лампы”, то есть, сколько исходов принадлежат интересующему нас событию?
Каждую интересующую нас пятерку можно составить так: выбрать две бракованные лампы, что можно сделать числом способов, равным 
. Каждая пара бракованных ламп может встретиться столько раз, сколькими способами ее можно дополнить тремя не бракованными лампами, то есть 
раз. Получается, что число пятерок, содержащих две бракованные лампы, равно 
×
.
Отсюда, обозначив искомую вероятность через
P, получаем (напоминаем,
):
1.3. Теоремы сложения и умножения вероятностей. Независимость событий. Условная вероятность.
Подробнее>>1.4. Статистическое определение вероятности
Рассмотрим случайный эксперимент, заключающийся в том, что подбрасывается игральная кость, сделанная из неоднородного материала. Ее центр тяжести не находится в геометрическом центре. В этом случае мы не можем считать исходы (выпадение единицы, двойки и т.д.) равновероятными. Из физики известно, что кость более часто будет падать
на ту грань, которая ближе к центру тяжести. Как определить вероятность выпадения, например, трех очков? Единственное, что можно сделать, это подбросить эту кость n раз (где n-достаточно большое число, скажем n=1000 или n=5000), подсчитать число выпадений трех очков n3 и считать вероятность исхода, заключающегося в выпадении трех очков, равной n3/n – относительной частоте выпадения трех очков. Аналогичным образом можно определить вероятности остальных элементарных исходов – единицы, двойки, четверки и т.д. Теоретически такой образ действий можно оправдать, если ввести статистическое определение вероятности.Вероятность P(w
i) определяется как предел относительной частоты появления исхода w i в процессе неограниченного увеличения числа случайных экспериментов n, то есть
,
где m
n(w i) – число случайных экспериментов (из общего числа n произведенных случайных экспериментов), в которых зарегистрировано появление элементарного исхода w i.Так как здесь не приводится никаких доказательств, мы можем только надеяться, что предел в последней формуле существует, обосновывая надежду жизненным опытом и интуицией.
В практике очень часто возникают задачи, в которых какой-либо другой способ определения вероятности события, кроме статистического определения, найти невозможно или крайне трудно.
ЗАКОН БОЛЬШИХ ЧИСЕЛ – общий принцип, в силу которого совместное действие случайных факторов приводит при некоторых весьма общих условиях к результату, почти не зависящему от случая. Первым примером действия этого принципа может служить сближение частоты наступления случайного события с его вероятностью при возрастании числа испытаний (часто использующееся на практике, например, при использовании частоты встречаемости какого-либо качества респондента в выборке как выборочной оценки соответствующей вероятности).
Сущность закона больших чисел состоит в том , что при большом числе независимых опытов частота появления какого-то события близка к его вероятности.
2. Основы математической статистики
. Что такое математическая статистика?Математическая (или теоретическая) статистика опирается на методы и понятия теории вероятностей, но решает в каком-то смысле обратные задачи.
В теории вероятностей рассматриваются случайные величины с заданным распределением или случайные эксперименты, свойства которых целиком известны. Предмет теории вероятностей
– свойства и взаимосвязи этих величин (распределений).Но часто эксперимент представляет собой черный ящик, выдающий лишь некие результаты, по которым требуется сделать вывод о свойствах самого эксперимента. Наблюдатель имеет набор числовых (или их можно сделать числовыми) результатов, полученных повторением одного и того же случайного эксперимента в одинаковых условиях.
При этом возникают, например, следующие вопросы: Если мы наблюдаем одну случайную величину – как по набору ее значений в нескольких опытах сделать как можно более точный вывод о ее распределении?
Если мы наблюдаем одновременно проявление двух (или более) признаков, т.е. имеем набор значений нескольких случайных величин — что можно сказать об их зависимости? Есть она или нет? А если есть, то какова эта зависимость?
Часто бывает возможно высказать некие предположения о распределении, спрятанном в “черном ящике”, или о его свойствах. В этом случае по опытным данным требуется подтвердить или опровергнуть эти предположения (“гипотезы”). При этом надо помнить, что ответ “да” или “нет” может быть дан лишь с определенной степенью достоверности, и чем дольше мы можем продолжать эксперимент, тем точнее могут быть выводы. Наиболее благоприятной для исследования оказывается ситуация, когда можно уверенно утверждать о некоторых свойствах наблюдаемого эксперимента – например, о наличии функциональной зависимости между наблюдаемыми величинами, о нормальности распределения, о его симметричности, о наличии у распределения плотности или о его дискретном характере, и т.д.
Итак, о (математической) статистике имеет смысл вспоминать, если
Примером такой серии экспериментов может служить социологический опрос, набор экономических показателей или, наконец, последовательность гербов и решек при тысячекратном подбрасывании монеты.
Математической статистикой называется раздел прикладной математики, изучающий методы сбора, обработки и анализа экспериментальных данных.
Предметом исследования в математической статистике является совокупность объектов, однородных относительно некоторых признаков.
Например, мальчики 10 лет г. Уссурийска; пловцы-мастера спорта России.
Совокупность из всех объектов, объединенных этими признаками, называется генеральной. Задачей исследования является изучение признаков генеральной совокупности, которые определяются влиянием некоторых случайных факторов.
Например, изучение физической подготовленности мальчиков 10 лет г. Уссурийска.
Для решения задач исследования проводится эксперимент (измерение, тестирование, анкетирование), в результате которого получают значение некоторой случайной величины (результаты тестирования, количество баллов). Если в эксперименте участвуют все объекты генеральной совокупности, то такое обследование называют сплошным.
На практике обычно применяют выборочный метод, который заключается в том, что из генеральной совокупности случайным образом извлекают n элементов. Эти элементы называются выборочной совокупностью или выборкой. Количество элементов в выборке называется ее объемом. Исследователь изучает и анализирует выборочную совокупность и на основании полученных показателей делает вывод о параметрах генеральной совокупности.
2.2. Методы группировки экспериментальных данных
Допустим, из генеральной совокупности извлечена выборка объемом n, измерена некоторая величина Х, в результате чего получен ряд значений х
1, х2, . . . хn. Этот ряд называется простым статистическим рядом.Пример: измерена масса тела 10 девочек 6 лет. Полученные данные образуют простой статистический ряд:
24 22 23 28 24 23 25 27 25 25
Отдельные значения статистического ряда называются вариантами. Если варианта х
i появилась m раз, то число m называют частотой, а ее отношение к объему выборки m/n – относительной частотой.Последовательность вариант, записанная в возрастающем (убывающем) порядке, называется ранжированным рядом
.Пример: Ранжированный ряд:
22 23 23 24 24 25 25 25 27 28
Таблица, в первой строке которой записаны все значения величины (варианты), во второй –- соответствующие им частоты, называется безынтервальным вариационным рядом.
Пример: Безынтервальный вариационный ряд
|
Х |
22 |
23 |
24 |
25 |
27 |
28 |
|
m |
1 |
2 |
2 |
3 |
1 |
1 |
Графическим изображением безынтервального вариационного ряда является полигон (рис. 1).
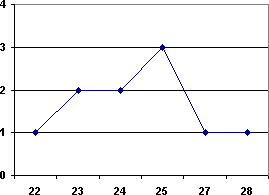
Рис. 1. Полигон вариационного ряда
Для его построения на оси ОХ откладывают значения вариант, на оси ОУ –- соответствующие им частоты. Точки с координатами (х
i; mi) соединяют отрезками, полученная ломаная линия называется полигоном частот.В том случае, если выборка представлена большим количеством различных значений непрерывной случайной величины, то группировку данных проводят в виде интервального вариационного ряда. Для этого диапазон варьирования признака разбивают на несколько (5-10) равных интервалов и указывают количество вариант, попавших в каждый интервал.
Алгоритм построения интервального вариационного ряда.
1. Исходя из объема выборки n, определить количество интервалов k.
|
n |
25-40 |
40-60 |
60-100 |
100-200 |
>200 |
|
k |
5-6 |
6-8 |
7-10 |
8-12 |
10-15 |
2. Вычислить размах ряда: R=X
max-Xmin3. Определить ширину интервала:
h=R/(k-1)4. Найти начало первого интервала X
0 = Xmin - h/25. Составить интервальный вариационный ряд.
Пример: измерена масса тела 100 женщин 30 лет, получены значения от 60 до 90 кг.
|
интервалы |
60-65 |
65-70 |
70-75 |
75-80 |
80-85 |
85-90 |
|
количество |
14 |
34 |
29 |
15 |
6 |
2 |
Размах ряда: R=X
max-Xmin=90-60=30Ширина интервала: h=R/(k-1)=30/5=6
Интервальный вариационный ряд:
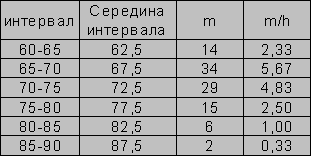
Графическим изображением интервального вариационного ряда является гистограмма. Для ее построения на оси ОХ откладывают интервалы шириной h, на каждом интервале строят прямоугольник высотой m/h. Величина m/h называется плотностью частоты. Гистограмма является эмпирическим аналогом графика дифференциальной функции распределения.
