Суммой (объединением) двух событий А и B (обозначается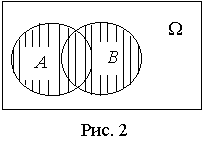 ) называется событие, состоящее из всех элементарных исходов, принадлежащих по крайней мере одному из событий А или B. Объединение событий А и В изображено на рисунке 2 в виде заштрихованной области.

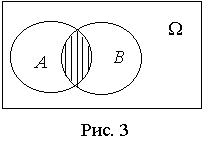
Приведем пример объединения событий. Пусть два стрелка стреляют в мишень одновременно, и событие А состоит в том, что в мишень попадает 1-й стрелок, а событие B – в том, что в мишень попадает 2-й. Событие означает, что мишень поражена, или, иначе, что в мишень попал хотя бы один из стрелков.

Произведением (пересечением) событий А и B называется событие, состоящее из всех тех элементарных исходов, которые принадлежат и А и B. На рисунке 3 пересечение событий А и B изображено в виде заштрихованной области. В условиях приведенного выше примера событие заключается в том, что в мишень попали оба стрелка.

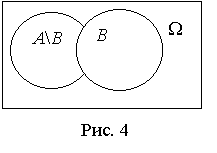
Разностью А\B или А–B событий А и B называется событие, состоящее из всех исходов события А, не благоприятствующих событию B. Диаграмма Венна разности событий А и B изображена на рисунке 4.

В условиях рассмотренного выше примера событие А\B заключается в том, что первый стрелок попал в мишень, а второй промахнулся.

Событие W называется достоверным (оно обязательно происходит в результате случайного эксперимента).

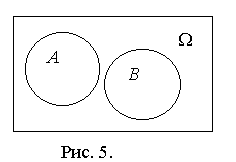
Пустое множество Æ называется невозможным событием. Событие =W \A называется противоположным событию А или дополнением события А.

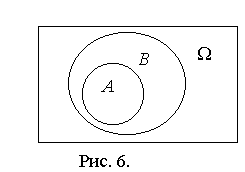
События А и B называются несовместными, если нет исходов, принадлежащих и А и B, то есть  = Æ . На рисунке 5 изображены несовместные события А и B.

Событие В будем называть следствием события А, если все исходы события А благоприятствуют событию В. То, что из А следует В записывается символом АÌ В и изображается на диаграмме Венна так, как это показано на рисунке 6.

Непосредственно из введенных определений следуют равенства: ; A=Æ ; ; . Два последних равенства называются формулами Де'Моргана.

Теоремы сложения и умножения вероятностей. Независимость событий. Условная вероятность.

1. Три стрелка стреляют по одной мишени, и каждый попадает или промахивается независимо от результатов выстрелов других стрелков. Вероятности попадания в мишень для каждого из стрелков, соответственно, равны: 0,8; 0,7; 0,5. Определить вероятности следующих событий:

а) все три стрелка попали в мишень;

б) хотя бы один стрелок попал в мишень;

в) в мишень попали два стрелка.

Решение.

а) Так как здесь рассматриваются независимые события, вероятность попадания в мишень всех трёх стрелков равна произведению вероятностей попадания каждого:

P = 0,8´ 0,7´ 0,5 = 0,28

б) Обозначим это событие А. Ему благоприятствует несколько несовместимых исходов, например, такой: {первый стрелок попал в мишень, второй не попал, третий попал}. Вместо того, чтобы рассматривать все эти исходы, возьмём событие – дополнение события А или, иначе, событие, противоположное событию А. Оно состоит в том, что все три стрелка не попали в мишень. Его вероятность равна:

(1 – 0,8) ´ (1 – 0,7) ´ (1 – 0,5) = 0,5

Теперь можно определить вероятность интересующего нас события:

Р(А) = 1 – Р() = 1 – 0,5 = 0,5

в) Этому событию благоприятствуют три исхода:

* {первый попал, второй попал, третий не попал} – c вероятностью

0,8 ´ 0,7 ´ (1 – 0,5) = 0,28

** {первый попал, второй не попал, третий попал} – c вероятностью

0,8 ´ (1 – 0,7) ´ 0,5 = 0,12

*** {первый не попал, второй попал, третий попал} – c вероятностью

(1 – 0,8) ´ 0,7 ´ 0,5 = 0,07

Очевидно, что эти исходы несовместимы, и поэтому вероятность их объединения, представляющего собой событие А, равна сумме их вероятностей:

Р(А) = 0,28 + 0,12 + 0,07 = 0,47

2. Брошено три игральных кости. Найти вероятности следующих событий:

а) выпало три шестёрки;

б) выпало три шестёрки, если известно, что на одной из костей выпала шестёрка.

Решение.

а) Здесь ответ очевиден:

б) Обозначим через А событие, состоящее в выпадении трёх шестёрок, а через В – в выпадении шестёрки хотя бы на одной кости. Тогда Р(А/В) – искомая вероятность. Событие АÇ В в данном случае совпадает с событием А, откуда следует: Р(АÇ В) = . Вероятность события В равна разности единицы и вероятности события , противоположного событию В, то есть выпадения трёх чисел, отличных от шестёрки. Вероятность равна . Отсюда следует: Р(В) = . В результате получается:

Р(А/В) =

3. Из 20 студентов, находящихся в аудитории, 8 человек курят, 12 носят очки, а 6 и курят и носят очки. Одного из студентов вызвали к доске. Определим события А и В следующим образом: A = {вызванный студент курит}, B = {вызванный носит очки}.

Установить, зависимы события A и B или нет. Сделать предположение о характере влияния курения на зрение.

Решение. Так как , то условие независимости не выполняется, следовательно, события A и B зависимы.

Найдем условную вероятность того, что студент носит очки, при условии, что он курит: . Безусловная вероятность того, что студент носит очки, равна . Так как , то делаем вывод: курение способствует ухудшению зрения.

5. Студент знает 20 из 25 вопросов программы. Зачёт сдан, если студент ответит не менее чем на 3 из 4-х вопросов в билете. Взглянув на первый вопрос, студент обнаружил, что знает его. Какова вероятность, что студент сдаст зачёт?

Решение.

Пусть А – событие, заключающееся в том, что студент сдал зачет;

В – событие, заключающееся в том, что студент знает первый вопрос в билете.

Очевидно, что р(В) = . Теперь необходимо определить вероятность р(АÇ В). Из 25-ти вопросов всего можно составить различных билетов, содержащих 4 вопроса. Все билеты, выбор которых удовлетворял бы и событию А и событию В, должны быть составлены следующим образом: либо студент знает все вопросы билета (можно составить всего таких билетов), либо студент знает первый, второй и третий вопросы, но не знает четвёртого (можно составить всего 5 таких билетов), либо студент знает первый, второй и четвёртый вопросы, но не знает третьего (тоже 5 билетов), либо студент знает первый, третий и четвёртый вопросы, но не знает второго (тоже 5 билетов). Отсюда получаем, что

р(АÇ В) =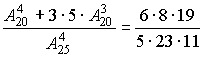

Осталось только найти искомую вероятность р(А/В):

р(А/В) = .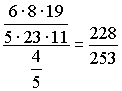

 

Оценка параметров генеральной совокупности

Характеристики положения

Основными параметрами генеральной совокупности являются математическое ожидание (генеральная средняя) М(Х) и среднее квадратическое отклонение s . Это постоянные величины, которые можно оценить по выборочным данным. Оценка генерального параметра, выражаемая одним числом, называется точечной.

Точечной оценкой генеральной средней m является выборочное среднее . Выборочным средним называется среднее арифметическое всех значений величины, встречающихся в выборке.

Если выборочное среднее вычисляется по несгруппированным данным, то для его определения сумму всех значений делят на количество элементов в выборке:

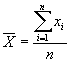
Пример: Вычислить среднее значение массы тела девочек 6 лет.

Если выборочное среднее вычисляется по вариационному ряду, то находят сумму произведений вариант на соответствующие частоты, и делят на количество элементов в выборке.

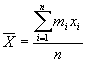
Пример: Вычислить среднее значение массы тела девочек 6 лет(ранжированный ряд – 22 23 23 24 24 25 25 25 26 27).

В том случае, когда статистические данные представлены в виде интервального вариационного ряда, при вычислении выборочного среднего значениями вариант считают середины интервалов.

Пример: вычислить среднее значение массы тела женщин 30 лет.

Выборочное среднее является основной характеристикой положения, показывает центр распределения совокупности, позволяет охарактеризовать исследуемую совокупность одним числом, проследить тенденцию развития, сравнить различные совокупности.

Непараметрическими характеристиками положения являются мода и медиана. Модой называется варианта, имеющая наибольшую частоту (для последнего примера мода равна 67,5).

Медианой называется варианта, расположенная в центре ранжированного ряда. Если ряд состоит из четного числа вариант, то медианой считают среднее арифметическое двух вариант, расположенных в центре ранжированного ряда.

Пример: найти моду и медиану выборочной совокупности по массе тела девочек 6 лет

Мо = 25; Ме = 24,5